En ciertas ocasiones, nos vemos en la necesidad de abordar un problema desde la base, partir de cero y diseñar paso a paso un protocolo para resolverlo de la forma más eficiente posible. Esto ocurre, por ejemplo, en el campo de la bioinformática, donde ciertos problemas pueden requerir un planteamiento independiente a pesar de ser de la misma naturaleza que otros muchos. En estos casos y en otros tantos (modelización matemática, ingeniería, estadística, etc) es necesario comenzar a trabajar a nivel de algoritmo para poder alcanzar soluciones válidas y sobre todo viables (en tiempo y recursos) a nuestro problema.
Es por ello que habitualmente una de las preocupaciones principales a la hora de diseñar un algoritmo es cómo de rápido funcionará. Y en este punto es habitual encontrar a quien piensa que una serie de medidas puntuales en una máquina concreta pueden arrojar resultados significativos y extrapolables a otras máquinas. Error, gran error. La forma de evaluar la eficiencia de un algoritmo debe ser universal (independiente de hardware) y además estar basada en el funcionamiento natural de cualquier algoritmo, las operaciones. Así, lo mas lógico es tratar de comprender y evaluar el número de operaciones que nuestro algoritmo llevará a cabo. Y de igual forma, la cantidad de memoria que el algoritmo necesitará para funcionar. Imaginemos un algoritmo sencillo que opera sobre dos strings de tamaños m y n, comparando su contenido. En este caso, el número de operaciones es proporcional al producto del tamaño de los inputs (los strings) y podemos afirmar que el algoritmo es de orden m·n. En caso de que ambos fueran del mismo tamaño, estaríamos hablando de un algoritmo de orden m². Tanto en un caso como en otro, la notación utilizada es la denominada big-O-notation, siendo O(mn) para el primer caso y O(m²) para el segundo. También cabe la posibilidad de que la eficiencia del algoritmo sea independiente del tamaño del input (por ejemplo, acceder al índice de un array) lo cual se denotaría O(1), o que la dependencia sea de tipo polinómico, exponencial, etc.
Es fundamental comprender la complejidad de cada algoritmo candidato para así poder evaluar cuál va a ser la diferencia en cuanto a eficiencia entre unos y otros. Por ejemplo, un algoritmo de orden exponencial duplica el número de operaciones con un input n+1 en comparación a un input n. Es posible que te permita realizar un análisis exhaustivo de tus datos, pero también que el número de operaciones que requiera para inputs moderados sea inaceptable. Un breve resumen qué tipo de algoritmo aumenta su complejidad más al aumentar el input sería:
n! > 2^n > n³ > n² > n·log n > log n > 1
Por todo lo anterior, a la hora abordar el diseño del algoritmo debemos considerar siempre el mejor caso (donde el algoritmo sea exigido en sus mínimos), caso promedio y peor de los casos, para poder determinar si el algoritmo va a poder ser implementado y ejecutado para resolver nuestro problema concreto. En ocasiones, el problema nos permitirá movernos en el mejor de los casos la mayor parte de las veces y pocas en el peor de los casos, pero puede haber otras ocasiones en que ocurra al revés, y debe ser algo a tener siempre en cuenta para cada problemática en particular.
En definitiva, se trata de evaluar cómo va a responder el algoritmo en términos universales y considerando siempre todos los casos posibles de uso, para así asegurar que su futura implementación y funcionamiento ocurran acordes a las necesidades y limitaciones inherentes al problema que enfrentamos. Más vale invertir algo más de tiempo en diseñar un buen algoritmo, que hacerlo a la ligera y tener que tirar todo el trabajo de implementación porque al final resulta no ser viable. Evaluad, valorad y entonces y sólo entonces, implementad.
Happy hacking!

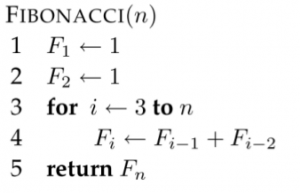

5 ideas sobre “Big-O-notation: evalúa el rendimiento de tus algoritmos”
Desde luego que nivel, Fibonacci, bioinformatica, algoritmos, esto es hacking de alto nivel, muy interesante y como no tengo muchos conocimientos sobre estos asuntos tengo una pregunta ¿esto se aplica para comprobar el correcto funcionamiento de los algoritmos de cifrado?
Un saludo
Jajajajaja qué exagerado, en realidad de alto nivel tiene poco. Lo de Fibonacci viene de que para explicar estas cosas se suele utilizar un ejemplo de la aplicación de un algoritmo iterativo versus uno recursivo para calcular la sucesión de Fibonacci y así comparar el diferente orden de cada uno de ellos, nada más.
De lo que me preguntas, no lo sé a ciencia cierta, pero por lógica diría que sí, aunque no para evaluar su correcto funcionamiento sino más bien para ver cómo de eficiente será el algoritmo a la hora de acometer la tarea de cifrado, o si es o no válido para X o Y tipo de cifrado.
Como siempre, un placer leerte por aquí 😉
Jajaja soy así, era una duda que se me ocurrió al vuelo, pero muy bien resuelta, estos temas me gustan, pero muchas veces se me escapa para que se aplican.
Gracias como siempre 😉
Mejor invertir en un buen algoritmo que en una buena máquina.
Un gran post bro, de esos que te hacen darle unas vueltas a la cabeza y pensar… 😉